publications

2025

1. 

   Variational Deep Learning via Implicit Regularization

   Jonathan Wenger, Beau Coker, Juraj Marusic, and John P. Cunningham

   In Pending review 2025

   Abs PDF

   Modern deep learning models generalize remarkably well in-distribution, despite being overparametrized and trained with little to no \emphexplicit regularization. Instead, current theory credits \emphimplicit regularization imposed by the choice of architecture, hyperparameters and optimization procedure. However, deploying deep learning models out-of-distribution, in sequential decision-making tasks, or in safety-critical domains, necessitates reliable uncertainty quantification, not just a point estimate. The machinery of modern approximate inference — Bayesian deep learning — should answer the need for uncertainty quantification, but its effectiveness has been challenged by our inability to define useful \emphexplicit inductive biases through priors, as well as the associated computational burden. Instead, in this work we demonstrate, both theoretically and empirically, how to regularize a variational deep network \emphimplicitly via the optimization procedure, just as for standard deep learning. We fully characterize the inductive bias of (stochastic) gradient descent in the case of an overparametrized linear model as generalized variational inference and demonstrate the importance of the choice of parametrization. Finally, we show empirically that our approach achieves strong in- and out-of-distribution performance without tuning of additional hyperparameters and with minimal time and memory overhead over standard deep learning.

2023

1. 

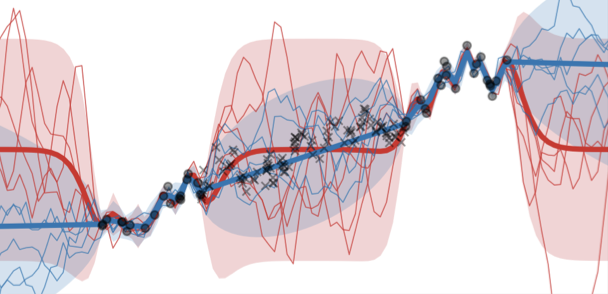   Implications of Gaussian process kernel mismatch for out-of-distribution data

   Beau Coker, and Finale Doshi-Velez

   In ICML workshops Spurious correlations, Invariance, and Stability (SCIS) and Structured Probabilistic Inference and Generative Modeling (SPIGM) 2023

   Abs PDF

   Gaussian processes provide reliable uncertainty estimates in nonlinear modeling, but a poor choice of the kernel can lead to poor generalization. Although learning the hyperparameters of the kernel typically leads to optimal generalization on in-distribution test data, we demonstrate issues with out-of-distribution test data. We then investigate three potential solutions– (1) learning the smoothness using a discrete cosine transform, (2) assuming fatter tails in function-space using a Student-t process, and (3) learning a more flexible kernel using deep kernel learning–and find some evidence in favor of the first two.

2022

1. 

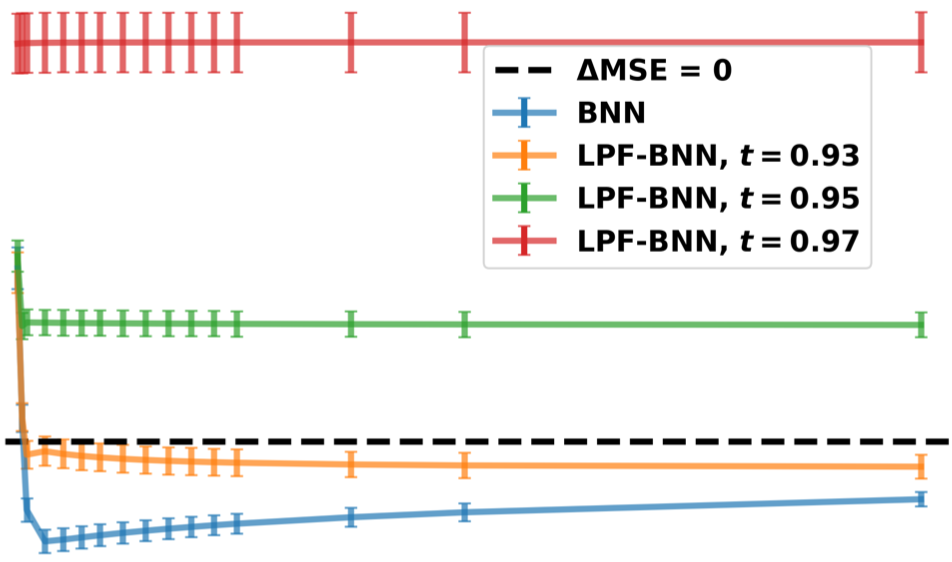   An Empirical Analysis of the Advantages of Finite v.s. Infinite Width Bayesian Neural Networks

   Jiayu Yao, Yaniv Yacoby, Beau Coker, Weiwei Pan, and Finale Doshi-Velez

   In NeurIPS Workshop on Gaussian Processes, Spatiotemporal Modeling, and Decision-making Systems 2022

   Abs PDF

   Comparing Bayesian neural networks (BNNs) with different widths is challenging because, as the width increases, multiple model properties change simultaneously, and, inference in the finite-width case is intractable. In this work, we empirically compare finite- and infinite-width BNNs, and provide quantitative and qualitative explanations for their performance difference. We find that when the model is mis-specified, increasing width can hurt BNN performance. In these cases, we provide evidence that finite-width BNNs generalize better partially due to the properties of their frequency spectrum that allows them to adapt under model mismatch.

2. 

   Towards a Unified Framework for Uncertainty-aware Nonlinear Variable Importance Estimation with Theoretical Guarantees

   Wenying Deng, Beau Coker, Rajarshi Mukherjee, Jeremiah Zhe Liu, and Brent A. Coull

   In Advances in Neural Information Processing Systems (NeurIPS) 2022

   Abs Bib PDF

   We develop a simple and unified framework for nonlinear variable importance estimation that incorporates uncertainty in the prediction function and is compatible with a wide range of machine learning models (e.g., tree ensembles, kernel methods, neural networks, etc). In particular, for a learned nonlinear model f(\mathbfx), we consider quantifying the importance of an input variable \mathbfx^j using the integrated partial derivative \Psi_j = \Vert \frac∂∂\mathbfx^j f(\mathbfx)\Vert^2_P_\mathcalX. We then (1) provide a principled approach for quantifying uncertainty in variable importance by deriving its posterior distribution, and (2) show that the approach is generalizable even to non-differentiable models such as tree ensembles. Rigorous Bayesian nonparametric theorems are derived to guarantee the posterior consistency and asymptotic uncertainty of the proposed approach. Extensive simulations and experiments on healthcare benchmark datasets confirm that the proposed algorithm outperforms existing classic and recent variable selection methods.

   @inproceedings{coker_neurips2022,
     title = {Towards a Unified Framework for Uncertainty-aware Nonlinear Variable Importance Estimation with Theoretical Guarantees},
     booktitle = {Advances in Neural Information Processing Systems (NeurIPS)},
     year = {2022},
     author = {Deng, Wenying and Coker, Beau and Mukherjee, Rajarshi and Liu, Jeremiah Zhe and Coull, Brent A.},
   }

3. 

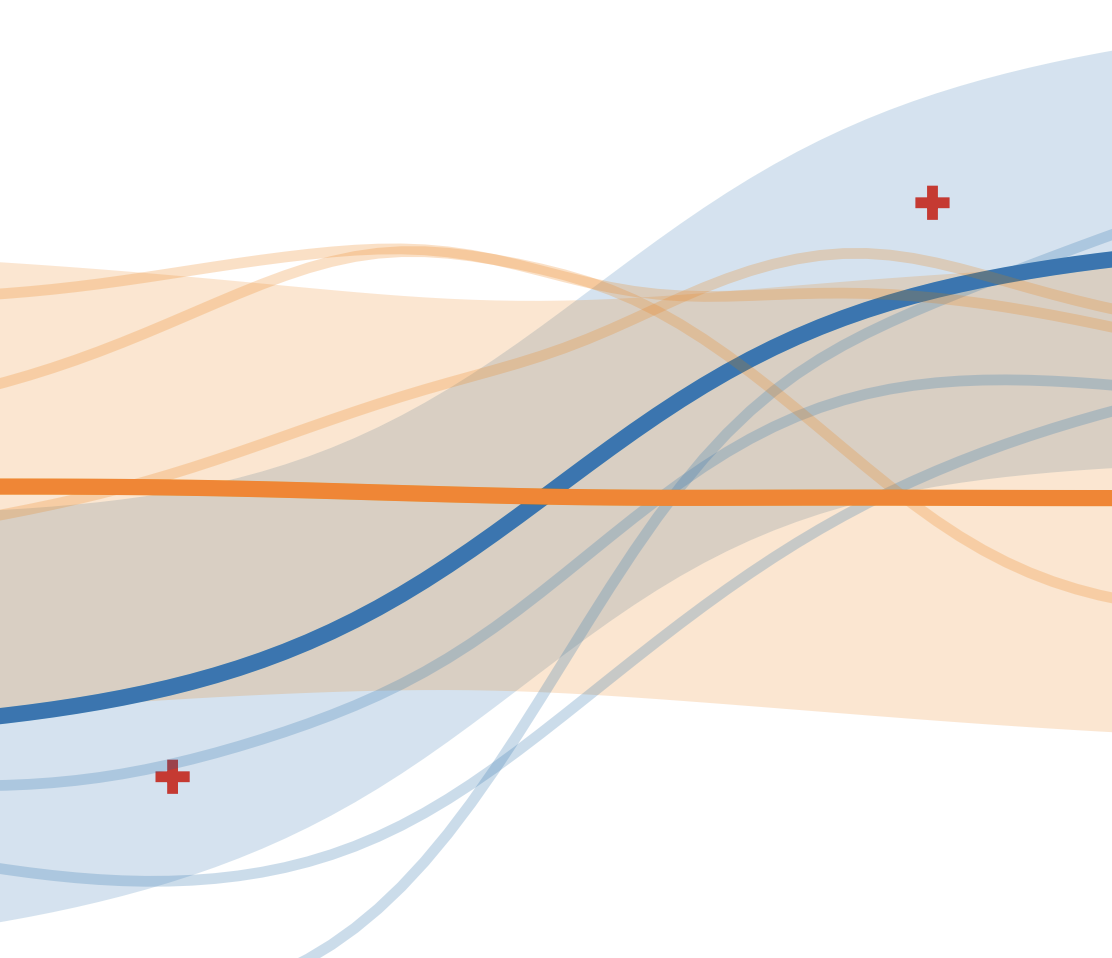   Wide Mean-Field Variational Bayesian Neural Networks Ignore the Data

   Beau Coker, Wessel P. Bruinsma, David R. Burt, Weiwei Pan, and Finale Doshi-Velez

   In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics (AISTATS) 2022

   Abs Bib PDF

   Bayesian neural networks (BNNs) combine the expressive power of deep learning with the advantages of Bayesian formalism. In recent years, the analysis of wide, deep BNNs has provided theoretical insight into their priors and posteriors. However, we have no analogous insight into their posteriors under approximate inference. In this work, we show that mean-field variational inference entirely fails to model the data when the network width is large and the activation function is odd. Specifically, for fully-connected BNNs with odd activation functions and a homoscedastic Gaussian likelihood, we show that the optimal mean-field variational posterior predictive (i.e., function space) distribution converges to the prior predictive distribution as the width tends to infinity. We generalize aspects of this result to other likelihoods. Our theoretical results are suggestive of underfitting behavior previously observered in BNNs. While our convergence bounds are non-asymptotic and constants in our analysis can be computed, they are currently too loose to be applicable in standard training regimes. Finally, we show that the optimal approximate posterior need not tend to the prior if the activation function is not odd, showing that our statements cannot be generalized arbitrarily.

   @inproceedings{coker_aistats2022,
     title = {Wide Mean-Field Variational Bayesian Neural Networks Ignore the Data},
     booktitle = {Proceedings of the 25th International Conference on Artificial Intelligence and Statistics (AISTATS)},
     year = {2022},
     author = {Coker, Beau and Bruinsma, Wessel P. and Burt, David R. and Pan, Weiwei and Doshi-Velez, Finale},
   }

2021

1. 

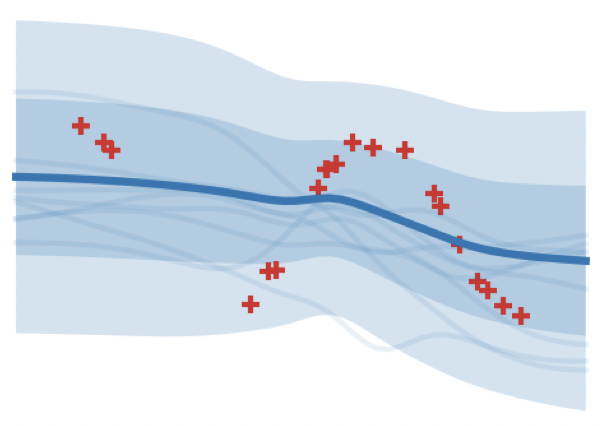   Wide Mean-Field Variational Bayesian Neural Networks Ignore the Data

   Beau Coker, Weiwei Pan, and Finale Doshi-Velez

   In ICML Workshop on Uncertainty and Robustness in Deep Learning 2021

   Abs Bib PDF

   Variational inference enables approximate posterior inference of the highly over-parameterized neural networks that are popular in modern machine learning. Unfortunately, such posteriors are known to exhibit various pathological behaviors. We prove that as the number of hidden units in a single-layer Bayesian neural network tends to infinity, the function-space posterior mean under mean-field variational inference actually converges to zero, completely ignoring the data (assuming it has been centered around zero). This is in contrast to the true posterior, which converges to a Gaussian process. Our work provides insight into the over-regularization of the KL divergence in variational inference.

   @inproceedings{coker_udl2021,
     title = {Wide Mean-Field Variational Bayesian Neural Networks Ignore the Data},
     booktitle = {ICML Workshop on Uncertainty and Robustness in Deep Learning},
     year = {2021},
     author = {Coker, Beau and Pan, Weiwei and Doshi-Velez, Finale},
   }

2. 

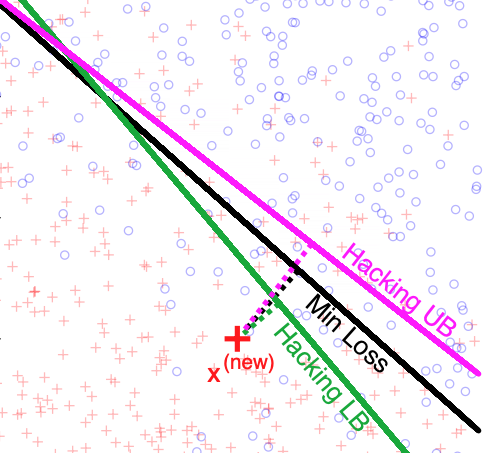   A Theory of Statistical Inference for Ensuring the Robustness of Scientific Results

   Beau Coker, Cynthia Rudin, and Gary King

   Management Science 2021

   Abs Bib HTML PDF

   Inference is the process of using facts we know to learn about facts we do not know. A theory of inference gives assumptions necessary to get from the former to the latter, along with a definition for and summary of the resulting uncertainty. Any one theory of inference is neither right nor wrong, but merely an axiom that may or may not be useful. Each of the many diverse theories of inference can be valuable for certain applications. However, no existing theory of inference addresses the tendency to choose, from the range of plausible data analysis specifications consistent with prior evidence, those that inadvertently favor one’s own hypotheses. Since the biases from these choices are a growing concern across scientific fields, and in a sense the reason the scientific community was invented in the first place, we introduce a new theory of inference designed to address this critical problem. We introduce hacking intervals, which are the range of a summary statistic one may obtain given a class of possible endogenous manipulations of the data. Hacking intervals require no appeal to hypothetical data sets drawn from imaginary superpopulations. A scientific result with a small hacking interval is more robust to researcher manipulation than one with a larger interval, and is often easier to interpret than a classical confidence interval. Some versions of hacking intervals turn out to be equivalent to classical confidence intervals, which means they may also provide a more intuitive and potentially more useful interpretation of classical confidence intervals.

   @article{coker_ms2018,
     author = {Coker, Beau and Rudin, Cynthia and King, Gary},
     year = {2021},
     volume = {67},
     number = {4},
     pages = {},
     title = {A Theory of Statistical Inference for Ensuring the Robustness of Scientific Results},
     journal = {Management Science},
     doi = {10.1287/mnsc.2020.3818},
   }

2020

1. 

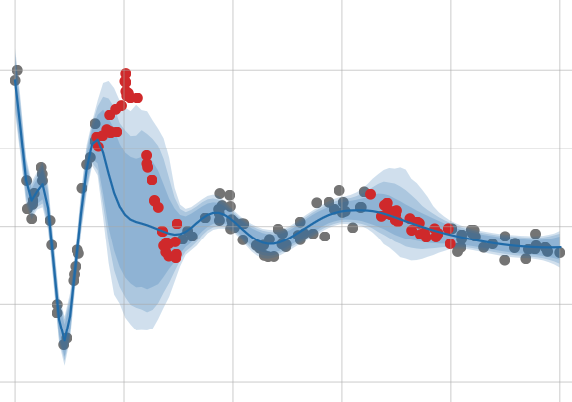   PoRB-Nets: Poisson Process Radial Basis Function Networks

   Beau Coker, Melanie Pradier, and Finale Doshi-Velez

   In Proceedings of the 36th Conference on Uncertainty in Artificial Intelligence (UAI) 2020

   Abs Bib PDF

   Bayesian neural networks (BNNs) are flexible function priors well-suited to situations in which data are scarce and uncertainty must be quantified. Yet, common weight priors are able to encode little functional knowledge and can behave in undesirable ways. We present a novel prior over radial basis function networks (RBFNs) that allows for independent specification of functional amplitude variance and lengthscale (i.e., smoothness), where the inverse lengthscale corresponds to the concentration of radial basis functions. When the lengthscale is uniform over the input space, we prove consistency and approximate variance stationarity. This is in contrast to common BNN priors, which are highly nonstationary. When the input dependence of the lengthscale is unknown, we show how it can be inferred. We compare this model’s behavior to standard BNNs and Gaussian processes using synthetic and real examples.

   @inproceedings{coker_uai2020,
     title = {PoRB-Nets: Poisson Process Radial Basis Function Networks},
     booktitle = {Proceedings of the 36th Conference on Uncertainty in Artificial Intelligence (UAI)},
     volume = {124},
     year = {2020},
     pages = {1338--1347},
     author = {Coker, Beau and Pradier, Melanie and Doshi-Velez, Finale},
   }

2. 

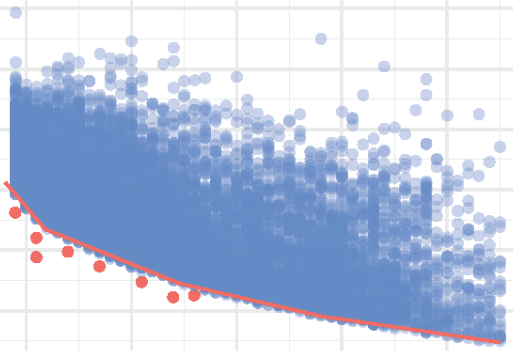   The Age of Secrecy and Unfairness in Recidivism Prediction

   Cynthia Rudin, Caroline Wang, and Beau Coker

   Harvard Data Science Review Mar 2020

   Abs Bib HTML

   In our current society, secret algorithms make important decisions about individuals. There has been substantial discussion about whether these algorithms are unfair to groups of individuals. While noble, this pursuit is complex and ultimately stagnating because there is no clear definition of fairness and competing definitions are largely incompatible. We argue that the focus on the question of fairness is misplaced, as these algorithms fail to meet a more important and yet readily obtainable goal: transparency. As a result, creators of secret algorithms can provide incomplete or misleading descriptions about how their models work, and various other kinds of errors can easily go unnoticed. By trying to partially reconstruct the COMPAS model—a recidivism risk-scoring model used throughout the criminal justice system—we show that it does not seem to depend linearly on the defendant’s age, despite statements to the contrary by the model’s creator. This observation has not been made before despite many recently published papers on COMPAS. Furthermore, by subtracting from COMPAS its (hypothesized) nonlinear age component, we show that COMPAS does not necessarily depend on race other than through age and criminal history. This contradicts ProPublica’s analysis, which made assumptions about age that disagree with what we observe in the data. In other words, faulty assumptions about a proprietary model led to faulty conclusions that went unchecked until now. Were the model transparent in the first place, this likely would not have occurred. We demonstrate other issues with definitions of fairness and lack of transparency in the context of COMPAS, including that a simple model based entirely on a defendant’s age is as ‘unfair’ as COMPAS by ProPublica’s chosen definition. We find that there are many defendants with low risk scores but long criminal histories, suggesting that data inconsistencies occur frequently in criminal justice databases. We argue that transparency satisfies a different notion of procedural fairness by providing both the defendants and the public with the opportunity to scrutinize the methodology and calculations behind risk scores for recidivism.

   @article{rudin_hdsr2020,
     journal = {Harvard Data Science Review},
     doi = {10.1162/99608f92.6ed64b30},
     number = {1},
     note = {https://hdsr.mitpress.mit.edu/pub/7z10o269},
     title = {The Age of Secrecy and Unfairness in Recidivism Prediction},
     url = {https://hdsr.mitpress.mit.edu/pub/7z10o269},
     volume = {2},
     author = {Rudin, Cynthia and Wang, Caroline and Coker, Beau},
     date = {2020-03-31},
     year = {2020},
     month = mar,
     day = {31},
   }

3. 

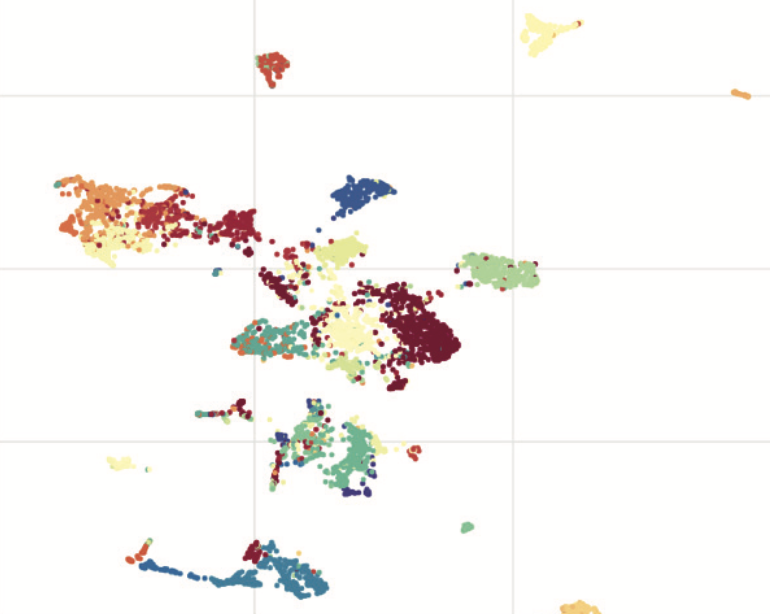   Learning a Latent Space of Highly Multidimensional Cancer Data

   Benjamin Kompa, and Beau Coker

   In Biocomputing Mar 2020

   Abs Bib PDF

   We introduce a Unified Disentanglement Network (UFDN) trained on The Cancer Genome Atlas (TCGA), which we refer to as UFDN-TCGA. We demonstrate that UFDN-TCGA learns a biologically relevant, low-dimensional latent space of high-dimensional gene expression data by applying our network to two classification tasks of cancer status and cancer type. UFDN-TCGA performs comparably to random forest methods. The UFDN allows for continuous, partial interpolation between distinct cancer types. Furthermore, we perform an analysis of differentially expressed genes between skin cutaneous melanoma (SKCM) samples and the same samples interpolated into glioblastoma (GBM). We demonstrate that our interpolations consist of relevant metagenes that recapitulate known glioblastoma mechanisms.

   @inproceedings{kompa_psb2020,
     author = {Kompa, Benjamin and Coker, Beau},
     title = {Learning a Latent Space of Highly Multidimensional Cancer Data},
     booktitle = {Biocomputing},
     chapter = {},
     pages = {379-390},
     year = {2020},
     doi = {10.1142/9789811215636_0034},
   }